Equações contendo derivadas – as equações diferenciais – são modelos matemáticos de muitos processos físicos. Movimentos de fluidos e de correntes elétricas, dissipação do calor em objetos sólidos, detecção de ondas sísmicas, são alguns desses processos. Procuro mostrar a gênese dos modelos matemáticos, com a contribuição da geometria e da álgebra no seu modo de formação. A abordagem é feita através do cálculo elementar, para que fique patente a sua natureza abstrata e geral. No final, o cálculo integral é citado apenas como o inverso do cálculo diferencial.
Aritmética, álgebra e cálculo são as grandes divisões da matemática. Nesta ordem é que ela é ensinada. No entanto os limites de cada uma dessas áreas não são bem definidos, por se tratar de uma expansão contínua do conhecimento matemático. Desta vez vou abordar o cálculo diferencial e integral e o que ele significa na teoria das funções. Função é o nome que se dá a uma relação de interdependência de duas ou mais variáveis numéricas, geralmente representada por uma curva. Baseia-se fundamentalmente no conceito de limite, implicando nas noções de continuidade, diferenciação e integração. A sua generalização supõe espaços abstratos, cujos elementos não são numéricos mas funções de funções. O estudo desses espaços é o objetivo da análise funcional. Essa expansão não será tratada agora. Deixemos isso para outra oportunidade.
Consideremos o círculo e seus elementos componentes, o centro, a circunferência e o raio. Como já disse, o ponto é uma figura geométrica adimensional, isto é, não tem dimensões. A circunferência, portanto, é constituída por um número infinito de pontos. Este conceito axiomático é o que garante a continuidade da linha curva da circunferência. Não existem intervalos, falhas ou quaisquer descontinuidades. A curva é contínua, ponto por ponto. Se no extremo de um raio, traçarmos uma linha reta que lhe seja perpendicular, ela é tangente à circunferência nesse ponto. Para nós, o termo tangente tem a conotação imediata da trigonometria, mas para os Gregos Pitagóricos a tangente tinha um significado puramente geométrico. Vejamos o que diz o matemático Alfred North Whitehead em “Introduction to Mathematics”, Oxford University Press, 1948: “Esta idéia geral de uma curva de exibir, em qualquer ponto, uma propriedade uniforme, é expressa na geometria pelo termo ‘locus’. Um locus é uma curva (ou superfície, se não nos confinarmos no plano), formada por pontos tendo todos uma determinada propriedade. Toda a propriedade, em relação a qualquer outra que os pontos possam ter, que corresponda a um locus, engloba todos os pontos que a possuem. Ao investigar as propriedades de um locus como um todo, podemos considerar qualquer ponto ou pontos do locus. Assim, na geometria, encontramos novamente a idéia fundamental de variável. Além disso, classificando os loci sob esses aspectos em linhas retas, círculos, elipses, etc., voltamos a encontrar a idéia de forma”.
Aplicando estes conceitos ao círculo, podemos defini-lo como o lugar geométrico de todos os pontos do plano eqüidistantes de um ponto chamado centro. Suponhamos que o raio e a sua perpendicular gire dando uma volta completa. O que dissemos para um ponto repete-se para qualquer outro ponto da curva circular. Quer dizer, a circunferência tem sempre a mesma curvatura qualquer que seja o ponto escolhido. Assim o raio de curvatura em qualquer ponto da circunferência, é o inverso da curvatura nesse ponto, ou seja, é o raio do círculo. Do mesmo modo, a elipse é o lugar geométrico dos pontos do plano, cuja soma das distâncias de qualquer um desses pontos a dois pontos fixos chamados focos, é constante. Assim, o círculo pode ser considerado como um caso particular da elipse, quando os dois pontos focais se superpõem no mesmo ponto. Desta forma, a soma das duas distâncias é igual a duas vezes o raio do círculo, quer dizer é a curvatura de uma curva fechada convexa, representada por um diâmetro, com tangentes nos seus extremos.
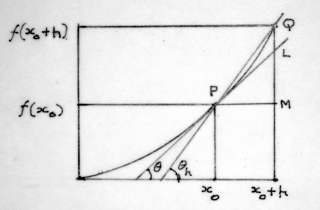
Seja y=f(x) uma função real de variável real, onde y é a variável dependente e x a variável independente. A derivada da função significa que existem dois conjuntos de elementos, ordenados de tal forma, que a um valor de x corresponde um e somente um valor de y. Não é obrigatório que seja o x a variável independente e o y a dependente. Pode ser o inverso desde que devidamente expresso, mas o usual é assim como disse. Além disso, a função existe, mesmo se a dois valores de x corresponder um só valor de y, mas não existe, se a um único valor de x corresponder dois valores de y. No início falamos do locus, o lugar geométrico dos pontos, o que quer dizer que existe uma propriedade geral abrangendo todos eles, ou seja, uma função. Como é essa função, só podemos saber obtendo a sua derivada, por ser ela que nos dá a taxa de variação dos valores pontuais. Por exemplo, a velocidade de um corpo em movimento, representado por um ponto, é a taxa da variação, em relação ao tempo, da posição desse ponto. Por sua vez, a aceleração, se existir, é a taxa da variação da taxa da variação da posição desse mesmo ponto, em relação ao tempo. No primeiro caso, é a 1ª derivada da função. No segundo caso, é a 2 ª derivada, isto é, a derivada da derivada. A derivada, portanto, diz-nos o tipo de curva que representa a função, ponto a ponto. De fato, derivada quer dizer “derivada da função f(x) no ponto xo”. A sua interpretação geométrica é a de uma tangente à curva nesse ponto. Mas como vimos no locus, um ponto isolado não é suficiente, por si só, para se obter uma definição. É preciso saber se a tangente se forma no limite, isto é, se a corda que passa pelo ponto dado e por um ponto imediatamente antes, se transforma na tangente, quando este se deslocar na curva, atingindo, no limite, o ponto dado. A interpretação geométrica da derivada pode ser obtida no plano ortogonal cartesiano, desenhando um trecho de curva voltada para um só lado (convexa para o eixo horizontal dos x’s por exemplo).
Marque, na curva, o ponto P de abscissa xo e pouco mais à frente, o ponto Q de abscissa xo+h. Ligando os pontos P e Q por uma linha reta obtemos uma corda da curva. Prolongue essa corda até atingir o eixo da abscissas. Temos portanto o ponto P de coordenadas xo e f(xo) e o ponto Q de coordenadas xo+h e f(xo+h). Se o ponto Q se deslocar na curva na direção de P, a distância h entre eles tende para zero e a diferença f(xo+h) – f(xo) tende para um número que é a derivada da função f(x) no ponto xo. Este é o conceito de limite em que se baseia a derivada. Para que ela exista, é necessário que o trecho da curva entre xo e xo+h seja uma curva circular. O ponto Q atinge o ponto P após percorrer, ponto por ponto, um número infinito de pontos. Se a curva for circular, ao atingir o ponto P a corda transforma-se numa tangente perpendicular ao seu raio de curvatura. Conseqüentemente, a linha reta tangente no ponto P, é a tangente trigonométrica do ângulo que essa reta faz com o eixo das abscissas.
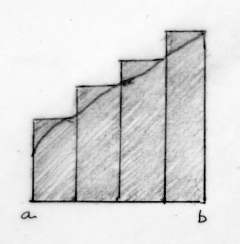
Suponhamos agora que repetimos a operação que foi descrita acima, numa seqüência de n vezes. Se f(x) tiver continuidade, o intervalo a,b será igual a n.h. Isto é, igual a n intervalos seguidos, todos da mesma largura. A esses intervalos marcados no eixo dos x’s correspondem n faixas verticais de largura h. Os lados dessas faixas interceptam a curva n+1 vezes, formando retângulos, em que cada retângulo tem os dois vértices superiores, um na curva e outro à sua distância h. Mas h pode ser tão pequeno quanto se queira. Portanto, podemos obter, no intervalo a,b, uma seqüência de tangentes à curva que representa a derivação da função nesse trecho. Se em vez das tangentes, nos preocuparmos com as áreas dos retângulos, temos então a integração da função nesse trecho, que é a operação inversa da diferenciação.
Fico por aqui. Até à próxima.